How is E-M radiation produced?
- Accelerate charged particles back and forth like they do at the radio station.
- All objects with temperature above "absolute zero" emit E-M radiation.
- Absolute Zero is the temperature where all motion (on the
atomic level) ceases.
- 0 Kelvin = -459º F = -273º C
- If a plot is made of the amount (intensity) of E-M radiation emitted at each
wavelength by a non-zero-temperature solid object, this is called a "spectrum".
For solids, the spectrum is called a Planck spectrum or a blackbody
spectrum. This is an important point!
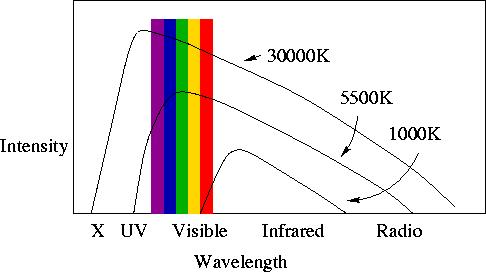
- For a given object, as the temperature increases:
- The intensity of radiation at all wavelengths increases.
- The peak of the intensity moves to shorter wavelengths (or higher
frequencies). You already knew this - think about your stove element as you
turn up the heat.
Wien's Law
The way the peak of the Planck curve changes with temperature is quantified by
Wien's Law .
This is Powerful!
- Measure the spectrum of the Sun (the intensity of E-M radiation at every
wavelength) and find:
max = 5500 Å = 5.5 x 10-5 cm
- Knowing this, we can estimate the surface temperature of the Sun from Wien's Law
(this will give the right answer if the solar spectrum does indeed look like a Planck
spectrum).
| Temp = |
0.29
|
= 5200 K |
| 5.5 x 10-5 |
Q. What about radiation from humans?
Note that the radiation we are all using to see one another is reflected from the
lights in the room. (Don't believe me? Turn off the lights and see what you see...)
Thumans ~ 300K
|
max(cm) = |
0.29
|
= 9.8 x 10-4 |
| T(K) |
= 9.8 µm  Infrared
Infrared
This is bad news for soldiers and out-of-bounds campers in Yosemite!
Q. What temperature needs to be reached for the Planck radiation of a solid to peak
in the x-ray region (~ 10-9 cm)?
| TX = |
0.29
|
= 2.9 x 108 K |
| 10-9 |
Note: solids don't ordinarily get this hot!
