STELLAR LUMINOSITIES

Remember that luminosity is the total amount of energy produced in a star and radiated into space in the form of E-M radiation. The Sun radiates 3.9 x 10 ³³ ergs/sec.   An "erg" is not a joke, it is a unit of energy

Start with the Sun

• How do we figure out the luminosity of the Sun?

  It's easy. Measure its (apparent) brightness, measure it's distance, and use the inverse square law.

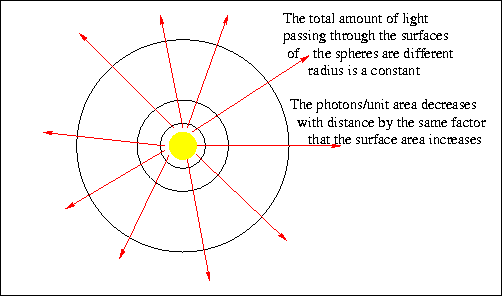
  The sun emits some amount of total energy from its surface every second (this is the luminosity of the sun). As that energy is radiated away from the sun, it passes through increasingly larger spherical areas. Since the total amount of energy passing through each sphere is the same, the energy per unit area decreases as the square of the distance (or the square of the radius of the sphere) from the sun. This is the inverse square law.
  

  

  The apparent brightness is a measure of photon energy passing through a square whatever at the distance of the Earth. One way to determine the total energy release in photons is to multiply the photon energy per square whatever, times the total area of the sphere with radius 1 AU (remember an astronomical unit is the distance between the Earth and Sun) in units of square whatevers.
  
  
  

• One measure of the apparent brightness of the Sun is the "Solar Constant".

  At the Earth's surface we receive:     1,400,000 ergs/square cm/second.

  (Note that a normal-sized human emits 100 watts in IR power.
  Strangely enough a black horse in a field on a sunny day absorbs around 800 watts = 1 horsepower).
  
  
  

• How about the top of this building?

  The energy beating down on the roof per second in solar photons is given by the solar constant times the roof area:
  

  (1.4 x 10⁶ ergs/cm²/sec)   x   (roof area)

  Roof Area:   100m x 100m   =   104 m2  x	100 cm2	=   108 cm2
  	1 m2

  So:    1.4 x 106	ergs	x   108 cm2	=   1.4 x 1014 ergs/sec
  	cm2 sec

  
  

  = 14MW (Mega-Watts)

  Is this alot? Total campus usage is 3.5 MW.
  
  
  

• So, given the solar constant, how do we find the total radiant energy of the Sun?

  We have the energy per square cm per second:   1.4 x 10⁶ ergs/cm²/sec

  The Surface Area of a sphere with radius R = 1AU is:

  4 R2 = 4 (1.5 x 1010 cm2 ) = 2.8 x 1027 cm 2

  
  
  

• The total energy flowing through the surface of this sphere is therefore:
  L   =   1.4 x 10⁶ ergs/cm²/sec   x   2.8 x 10²⁷ cm²   =   3.9 x 10³³ ergs/sec
  
  

  This is the total energy produced by the Sun   (L stands for solar luminosity).

  How much energy is this? It is pretty hard to get a feeling for numbers this large.
  At PG&E rates, the price of the Sun's energy would be 10¹⁹ $/sec

Can you answer these questions...

Q. What is the Solar Luminosity at the distance of Mars (1.5 AU)?

Still the same, 1 solar luminosity. The Martian "solar constant" will be smaller by a factor of 1.5 x 1.5, but added up over the entire surface of the sphere centered on the Sun with radius 1.5AU, the luminosity is the same. Luminosity is an intrinsic property of the Sun.

Q. What is the Solar Luminosity at the surface of the Sun?   Right, it's still 1 solar luminosity.

A REALLY GOOD QUESTION:

How does the Sun manage to produce all that energy and maintain that production for at least 4.5 billions years?

What about the Luminosity of those other stars?

Once we have the distance to any other star, we can combine that with the apparent brightness and the inverse-square law for light dimming to determine the "intrinsic brightness" or luminosity of the star.

We can therefore determine a luminosity for all the stars for which we have trigonometric parallax measurements.
You will find out that there is a pretty big range from 25 L down to 0.00001 L