ENERGY SOURCES FOR STARS

For the next week "we" will look at one of the most fundamental questions about a star:

How does a star produce all the energy that it radiates away into space?

The answer to this explains the existence of the main sequence in the H-R Diagram and leads into the next big topic - the formation and evolution of stars.

One Possible Energy Source:   Coal or Wood burning

• What is "burning"?   Burning is the conversion of molecular binding energy into E-M radiation
  
  Coal burning yields   ~   4 x 10¹² ergs/gram     (This is not very efficient!)

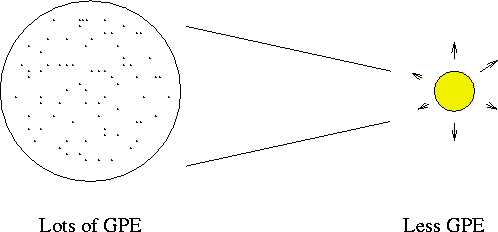
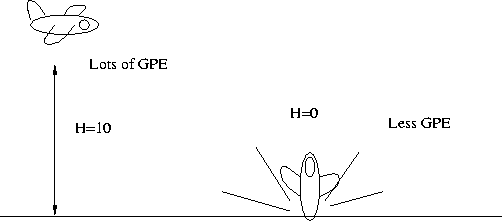
  So, a 3000 gram bucket of coal is good for about 1.2 x 10¹⁶ ergs or 300 Kilowatt-hours. This would run a little space heater for about an hour.

  Now, the Sun's mass is 2 x 10³³ grams. If the sun was made of coal and producing energy via conventional combustion, it could generate a total energy of:
  
  

  (4 x 10¹² ergs/gram)   x   (2 x 10³³ grams)   =   8 x 10⁴⁵ ergs
  
  

• The Question: How long would the Sun shine for the case of coal power?

  Lifetime is calculated by taking the total energy available divided by the rate at which you are using up the energy. The sun uses up energy at a rate of   1 L = 4 x 10³³ ergs/sec.
  

  Lifetime	=	8 x 1045 ergs   x	1 sec
  			4 x 1033 ergs
  	=	2 x 1012 secs   x	1 min	x	1 hr	x	1 day	x	1 year
  			60 sec		60 min		24 hr		365 days
  	=	6300 years

• Note: 1 L is equivalent to 1 ton of coal burned per hour for every square foot of the Sun's surface

• By the mid-1800's it was recognized that the Earth and Sun were at least millions of years old. This was a puzzle - the most common source of energy on Earth could not be used to explain the energy production and longevity of the Sun.

Another Possible Energy Source:   Gravitational Potential Energy

• What is gravitational potential energy?
  

  Anytime you have a collection of mass (for example a gas of atoms and molecules), it has an associated Gravitational Potential Energy - GPE. For a big ball of gas, the GPE goes like:

  GPE   =   -	3	x	M2	x	G
  	5		R

  where R is the radius of the ball of gas, M is the total mass, and G is the "gravitational constant".

  Similarly, because the Earth exerts a gravitational pull on objects at its surface and in space, these objects all have an associated GPE.
  
  

  • So, if a gas cloud shrinks in size without changing mass, it must release GPE. Energy is always conserved, so as a cloud shrinks, it heats up and emits radiation.
    
    
    

  • At the surface of the Earth, an object at a large radius from the center of the Earth has more GPE than the same object at a smaller radius (here the radius is the radius of the Earth plus the height of the object above the surface of the Earth)
    
    

  
  
  

• Perhaps the Sun is slowly shrinking in size and radiating away the lost GPE.

  How much total GPE does the Sun have that could be turned into radiation as the Sun shrinks?

  GPE   =	3	x	M2	x	G	~   2 x 1048 ergs
  	5		R

  This shows that converting GPE is a pretty efficient process compared to chemical burning:

  2 x 1048 ergs	=   1015 ergs/gram
  2 x 1033 grams

  This is about 250 times more efficient than chemical burning.
  
  
  

• OK, how long would the Sun last at its current luminosity if it was GPE powered?
  (Note that it would contract at about 40m per year)

  Lifetime   =   2 x 1048 ergs   x	1 sec	=   5 x 1014 sec
  	4 x 1033 ergs

  This converts to 16 million years - still too short!
  The Earth is around 4 billion years old (plus the Sun would have been much bigger in the past).

• Another possibility considered was the GPE of comets and meteors falling into the Sun. To produce L would require about 1 Earth mass per year to be accreted (not that much). This can be ruled out because the resulting change in the Earth's orbit has not been measured.