project two -- Burrau's problem of three bodies

"a proof walking on stilts, nay, a mean, underhand proof"

-Schopenhauer, Sammtliche Werke, I., sec. 15 (on Euclid's proof of the Pythagorean Theorem)

"My game is like the Pythagorean Theorem. No one has an answer"

-Shaquille O'Neill

In 1893, the mathematician Meissel from Kiel proposed a peculiar example of the problem of three bodies which has come to be known as the Pythagorean problem. The problem is simply stated:

Three point masses attract each other according to the Newtonian law of gravitation. The masses of the particles are m1=3, m2=4, and m3=5; they are initially located at the apexes of a right triangle with sides 3, 4, and 5, so that the corresponding masses and sides are opposite. The particles are free to move in the plane of the triangle and are at rest initially.

Meissel was of the opinion in 1893 that these initial conditions will lead to periodic motion. It is not clear how he arrived at this conjecture.

In 1913, Burrau, hoping to find a periodic solution attempted a numerical integration, with variable stepsize, and, over a limited period of motion, was unable to find an indication that the solution was periodic.

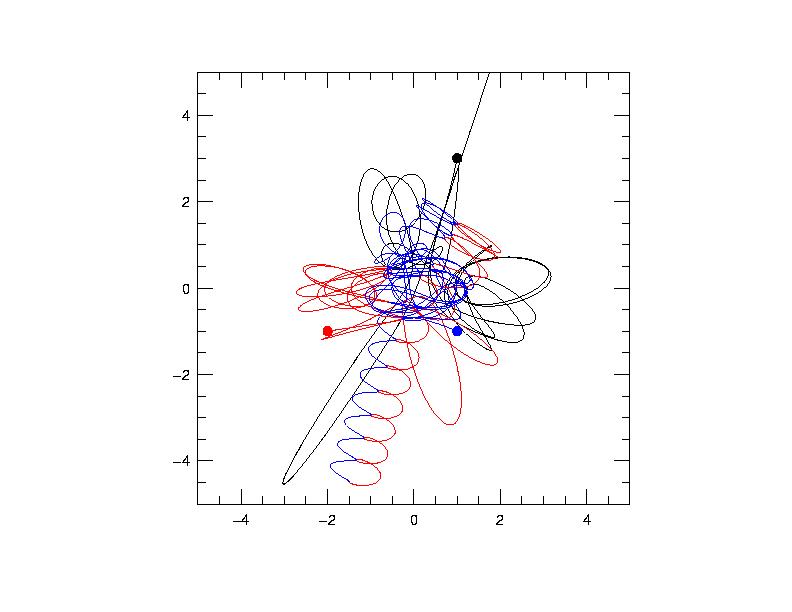
This problem was answered in 1967 with the advent of high-speed numerical integration and the technique of "two-body regularization" (see AY235) by Victor Szebehely and his collaborators. The solution is shown graphically in the picture above. The solution is neither quasi-periodic nor periodic, but rather assumes a form known in the technical literature as "elliptic-hyperbolic". After a great deal of action, the two heavy bodies form a bound binary pair, while the smaller body is ejected on a hyperbolic trajectory.

Szebeheley, in a highly engaging blow-by-blow description of the problem (see article 2 below) writes:

"One of the close approaches between m3 and m2 is almost a collision with nearly rectilinear orbits. At the same time, the velocity of m1 is close to zero. Such a combination of circumstances suggests the existence of a set of initial conditions leading to a periodic solution. This solution might start with zero velocities of the participating bodies - not in the Pythagorean configuration. At a time t=T/2<t0 when m2 and m3 collide and the velocity of m1 is zero, the solution reaches its half period. Then the motion is completely reversed and the bodies return to their original positions with zero velocity at time t=T."

Our problem is to use Levenberg-Marquardt variation of the initial parameters to find this periodic solution. We would then write up the solution, as well as context and historical background for submission to the Proceedings of the National Academy (see below).

resources

(1) Burrau, C., "Numerische Berechnung eines Spezialfalles des Dreikorperproblems" (A Numerical Solution to a Special Case of the Three-body Problem) Publickationer og mindre Meddelelser fra Kobenhavns Observatorium, No. 13 (1913); also, Astronomische Nachrichtung, 195 (4662), 113 (1913).

(2) The solution to the Pythagorean problem, as well as some notes on its history are written up in two papers by Szebehely:

Szebehely, V. 1967, "Burrau's Problem of Three Bodies", Proceedings of the National Academy of Sciences of the United States of America, vol. 58, Issue 1, pp. 60-65, postscript file here.

Szebehely, V. & Peters, C. F. 1967, "Complete Solution of a General Problem of Three Bodies", The Astronomical Journal, vol. 72., No. 7, pp. 876-883, postscript file here.

(3) A version of integrator.f configured to run the Pythagorean problem is here.