Summary of Previous Research:
The Structure and Dynamics of Elliptical Galaxies
(as of July 1999)
Postscript version
1. Introduction
Although our understanding of elliptical galaxies has improved dramatically in recent years,
there are still many important unresolved questions.
Not only is their formation history uncertain, but some of their fundamental
present-day properties are unknown ---
in particular, the shapes and radial profiles of their dark matter halos,
and the phase-space distribution of their stellar orbits.
I have been engaged in a series of theoretical studies using an array of modeling tools
in an effort to shed light on these questions.
(I am also working on a dynamical model of the Galactic center,
which I will not discuss in this summary.)
2. Deprojection Uncertainties in Axisymmetric Galaxies
The simplest of a galaxy's intrinsic properties, its three-dimensional lumino
sity
distribution \nu(r), is well determined observationally only under the assumption
of spherical symmetry.
For an axisymmetric galaxy, there is a ``cone of ignorance'' in Fourier space
that is
not sampled in projection,
so that the deprojection from the surface brightness I(R) to \nu is
in general not unique
(Rybicki 1987; Gerhard & Binney 1996; Kochanek & Rybicki 1996).
This deprojection degeneracy increases with inclination, from the edge-on case where
the solution is unique,
to the pole-on case where the galaxy's vertical structure is completely undetermined.
We set out to determine if a realistic galaxy could harbor
significant
``konus densities'' (density distributions that are invisible in projection),
and if so, to examine the effects on the galaxy's dynamics
(Romanowsky & Kochanek 1997).
Our deprojection algorithm is fully non-parametric,
and by construction guarantees the solution \nu
to be positive, and monotonic in the radial direction.
We used both simulated and real photometry data for elliptical galaxies.
We found that the deprojection uncertainty is very large, even at moderate inclinations,
with a variety of smooth, well-behaved solutions for \nu possible for a given galaxy image I;
the implied konus densities typically resembled disks
(see Figure 1).
Assuming a constant mass-to-light ratio and a two-integral distribution function,
we solved for the potential \Phi(r) and used the Jeans equations to find
the stellar velocities (radial and tangential) as a function of radius.
The solutions with and without a konus disk produced very different stellar dynamics,
but in projection these differences were attenuated, and were generally
undetectable with typical velocity measurement uncertainties.
The net conclusion is that significant dynamical subsystems can exist in early-type
galaxies and leave no detectable trace on the photometry and the projected velocities.
3. X-ray Isophote Twists
A promising avenue for observationally determining the distribution of dark matter
in early-type galaxies is by the analysis of X-ray emission from hot gas
in the halo potential.
Since various galaxy formation models make different predictions as to the final shapes
of the dark halos, it would be useful to determine the intrinsic shapes of halos
in real galaxies; in particular, how triaxial are they?
A radial gradient of the triaxiality of a galaxy's potential
(such as might arise from a difference in shape between the stellar and dark
matter components)
can produce a radial twist in the X-ray isophotes (Binney 1978; Buote & Canizares 1996),
analogous to the isophote twists seen in projected stellar light (Mihalas &
Binney 1981).
We have studied the characteristics of such twists in physically-motivated elliptical
galaxy models (Romanowsky & Kochanek 1998).
We numerically calculated the X-ray emission from simple model galaxies with
a variety of
stellar and halo shapes, and found that the axes of the X-ray isophotes follow
those of the projected mass to a very good approximation;
most of the isophote twist occurs inside the stellar effective radius Reff.
We used the shape parameters suggested by observations of stellar kinematics
(Franx et al. 1991)
and by simulations of halo formation (Dubinski & Carlberg 1991; Dubinski 1994)
to predict the distribution of X-ray twists expected for a large sample of galaxies.
We found that the prolateness of the halos in dissipationless simulations
implies
a mean total twist of
16°, while a 5° mean twist is implied by
the more oblate halos in simulations that include dissipation
(see Figure 2).
Current X-ray telescopes do not have sufficient resolution to see such twists
in galaxy cores,
but one could look for misalignments between the stellar and the outer
X-ray isophotes (at 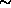 3 Reff), and thereby constrain the galaxy formation models.
We also examined the case of the elliptical galaxy NGC 720, which shows a sharp
X-ray isophote twist of
3 Reff), and thereby constrain the galaxy formation models.
We also examined the case of the elliptical galaxy NGC 720, which shows a sharp
X-ray isophote twist of 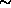 30° at 1-2 Reff (Buote & Canizares 1994, 1996).
This twist could not be reproduced by our models,
suggesting that the halo and the stars are intrinsically misaligned.
30° at 1-2 Reff (Buote & Canizares 1994, 1996).
This twist could not be reproduced by our models,
suggesting that the halo and the stars are intrinsically misaligned.
4. Stellar Dynamics of Lens Galaxies
In principle, measurements of the the time delay between the images in a gravitational
lens system can be used to directly determine the Hubble constant H0,
with none of the intermediate steps characterizing ``distance ladder'' approaches (Refsdal 1964).
The prototypical lens system Q0957+561 has a well-measured time delay
(e.g., Kundic et al. 1997),
but suffers from a ``mass sheet degeneracy'', where the mass in the system can be
traded between the lens galaxy and the surrounding cluster ---
an operation that does not affect the lensing observables,
but directly alters the derived value for H0
(Falco et al. 1985).
A measurement of the central stellar velocity dispersion
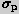 of the galaxy
(Falco et al. 1997)
could be used to independently find the galaxy mass, and thus break the degeneracy.
However, numerous theoretical studies have shown that the systematic uncertainty in converting
from a central
of the galaxy
(Falco et al. 1997)
could be used to independently find the galaxy mass, and thus break the degeneracy.
However, numerous theoretical studies have shown that the systematic uncertainty in converting
from a central
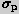 to a mass is enormous even for a spherical system, owing
to the unknown stellar velocity distribution anisotropy (Tonry 1983; Richstone & Tremaine 1984).
Previous models of this system have arrived at small systematic uncertainties
in this
conversion by making dubious assumptions about the anisotropy
(Grogin & Narayan 1996).
PG 1115+080 is the second system with a time delay (Schechter et al. 1997).
The lens galaxy's total mass is well constrained, but not its radial profile,
which again introduces a large systematic uncertainty in H0
(Impey et al. 1998).
A measurement of the galaxy's central
to a mass is enormous even for a spherical system, owing
to the unknown stellar velocity distribution anisotropy (Tonry 1983; Richstone & Tremaine 1984).
Previous models of this system have arrived at small systematic uncertainties
in this
conversion by making dubious assumptions about the anisotropy
(Grogin & Narayan 1996).
PG 1115+080 is the second system with a time delay (Schechter et al. 1997).
The lens galaxy's total mass is well constrained, but not its radial profile,
which again introduces a large systematic uncertainty in H0
(Impey et al. 1998).
A measurement of the galaxy's central
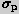 (Tonry 1998) may put useful constraints on the lens models.
(Tonry 1998) may put useful constraints on the lens models.
We have explored the stellar dynamics of these two lens galaxies
in order to set rigorous limits on H0 (Romanowsky & Kochanek 1999).
We used a very general spherical orbit modeling method
that fits a comprehensive library of stellar orbits in a given potential
to a set of stellar surface brightness and velocity data
(Schwarzschild 1979; Richstone & Tremaine 1984; Rix et al. 1997).
The resulting orbit solutions are non-parametric, and physical by constructio
n.
As expected, the range of permitted solutions for Q0957+561 is
large, resulting in a 73% uncertainty in the galaxy mass (and in H0).
To further constrain the mass, we placed observationally-motivated restrictions
on the line-of-sight velocity distribution (LOSVD);
the more extreme solutions can be ruled out by their peculiar LOSVDs.
To quantify these restrictions, we assembled a sample of 28 nearby elliptical
galaxies with
higher-order velocity moment measurements
(Bender et al. 1994),
and created ``mean profiles'' of the velocity dispersion
 and the fourth-order Gauss-Hermite moment h4(R).
The mean profiles are remarkably universal: the rms velocity profile is flat
to 1.5 Reff,
and the LOSVD is everywhere consistent with Gaussianity (h4=0).
Application of these profiles as constraints on the orbit model reduced the range
permitted for the mass (a 16% uncertainty),
which in combination with the Grogin & Narayan (1996) lens model yielded 2-\sigma
limits on H0 of
61-15+13 km s-1 Mpc-1.
Similarly, we applied the mean profile constraints to orbit models of the PG 1115+080 lens galaxy,
but found that none of the lens models (and their associated H0 values) could be ruled out.
and the fourth-order Gauss-Hermite moment h4(R).
The mean profiles are remarkably universal: the rms velocity profile is flat
to 1.5 Reff,
and the LOSVD is everywhere consistent with Gaussianity (h4=0).
Application of these profiles as constraints on the orbit model reduced the range
permitted for the mass (a 16% uncertainty),
which in combination with the Grogin & Narayan (1996) lens model yielded 2-\sigma
limits on H0 of
61-15+13 km s-1 Mpc-1.
Similarly, we applied the mean profile constraints to orbit models of the PG 1115+080 lens galaxy,
but found that none of the lens models (and their associated H0 values) could be ruled out.
5. Mass Distribution and Globular Cluster Dynamics in M87
The radial distribution of dark matter in elliptical galaxies has been generally difficult to
determine due to the dearth of unambiguous tracers of the potential at large radii.
Observational capabilities have recently been developed to obtain
large sets of velocity data for globular clusters (GCs) and planetary nebulae
around nearby galaxies.
Since these data can be taken at much larger radii than traditional stellar kinematic
measurements, with proper modeling they are powerful tools for probing the halo potential.
The nearby giant elliptical M87 (= NGC 4486) is the first galaxy to have available a large enough number of
GC data to begin putting robust constraints on the halo's radial profile
(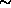 220 velocities; c.f. Merritt & Tremblay 1993).
220 velocities; c.f. Merritt & Tremblay 1993).
We are constructing galaxy models to fit
the surface brightness and velocity data for both the GCs
(e.g., Harris 1986; Lauer & Kormendy 1986; McLaughlin 1995; Mould et al. 1990;
Cohen & Ryzhov 1997)
and the stars
(Caon et al. 1990; Lauer et al. 1992; van der Marel 1994;
Sembach & Tonry 1996).
We hope that the combination of these data over a broad radial range
(R 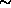 0"-500",
where Reff
0"-500",
where Reff 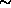 100")
will provide strong constraints on the dark matter distribution.
We will attempt to rigorously rule out a constant mass-to-light ratio model,
and we will examine the suitability of the halo profiles from hierarchical clustering simulations
(e.g., Navarro, Frenk, & White 1996)
for describing the dark matter distribution in M87.
We employ the spherical orbit modeling method described above,
extending it to include the discrete velocities of the GCs
(see Figures 3 and 4).
This method makes full use of the high-velocity tail of the GC LOSVD
in order to probe the depth of the potential.
100")
will provide strong constraints on the dark matter distribution.
We will attempt to rigorously rule out a constant mass-to-light ratio model,
and we will examine the suitability of the halo profiles from hierarchical clustering simulations
(e.g., Navarro, Frenk, & White 1996)
for describing the dark matter distribution in M87.
We employ the spherical orbit modeling method described above,
extending it to include the discrete velocities of the GCs
(see Figures 3 and 4).
This method makes full use of the high-velocity tail of the GC LOSVD
in order to probe the depth of the potential.
We will also examine the orbit structure of the globular cluster system (GCS)
in search of clues to its formation history.
It has long been known that the GCS of M87 has a much larger core radius than the
stellar distribution, and that the galaxy has an unusually high number of GCs for
its luminosity.
Furthermore, there is a clear bimodal distribution of the GCs, with differing
colors, metallicities, and radial distributions (e.g., Lee & Geisler 1993),
similar to what is seen in other galaxies
(Forbes et al. 1997).
To explain these features, there have been a variety of different scenarios
proposed for GC formation, accretion, destruction, etc. (see Harris 1998 for
a review).
By examining separately the dynamics of the two GC subsystems, we hope to provide
some insight on their formation histories, and by inference on the formation history
of the galaxy itself.
References
Bender, R., Saglia, R. P., & Gerhard, O. E. 1994, MNRAS, 269, 785
Binney, J. 1978, Comments Astrophys., 8, 27
Buote, D. A., & Canizares, C. R. 1994, ApJ, 427, 86
Buote, D. A., & Canizares, C. R. 1996, ApJ, 468, 184
Caon, N., Capaccioli, M., & Rampazzo, R. 1990, A&AS, 86, 429
Cohen, J. G., & Ryzhov, A. 1997, ApJ, 486, 230
Dubinski, J. 1994, ApJ, 431, 617
Dubinski, J., & Carlberg, R. G. 1991, ApJ, 378, 496
Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1
Forbes, D. A., Brodie, J. P., & Grillmair, C. J. 1997, AJ, 113, 1652
Franx, M., Illingworth, G., & de Zeeuw, T. 1991, ApJ, 383, 112
Gerhard, O., & Binney, J. 1996, MNRAS, 279, 993
Grogin, N. A., & Narayan, R. 1996, ApJ, 464, 92 (erratum 473, 570)
Harris, W. E. 1998, in ASP Conf. Ser. 136, Galactic Halos, ed. D. Zaritsky (San Francisco: ASP), 33
Harris, W. E. 1986, AJ, 91, 822
Impey, C. D., Falco, E. E., Kochanek, C. S., Lehar, J., McLeod, B. A., Rix, H.-W., Peng, C. Y., & Keeton, C. R. 1998, astro-ph/9803207
Kochanek, C. S., & Rybicki, G. B. 1996, MNRAS, 280, 1257
Kundic, T., Turner, E. L., Colley, W. N., et al. 1997, ApJ, 482, 75
Lauer, T. R., Faber, S. M., Lynds, C. R., et al. 1992, AJ, 103, 703
Lauer, T. R., & Kormendy, J. 1986, ApJ, 303, L1
Lee, M. G., & Geisler, D. 1993, AJ, 106, 493
van der Marel, R. P. 1994, MNRAS, 270, 271
McLaughlin, D. E. 1995, AJ, 109, 2034
Merritt, D., & Tremblay, B. 1993, AJ, 106, 2229
Mihalas, D., & Binney, J. 1981, Galactic Astronomy (New York: Freeman)
Mould, J. R., Oke, J. B., de Zeeuw, P. T., & Nemec, J. M. 1990, AJ, 99, 1823
Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563
Refsdal, S. 1964, MNRAS, 128, 307
Richstone, D. O., & Tremaine, S. 1984, ApJ, 286, 27
Rix, H.-W., de Zeeuw, P. T., Cretton, N., van der Marel, R. P., & Carollo, C. M. 1997, ApJ, 488, 702
Romanowsky, A. J., & Kochanek, C. S. 1997, MNRAS, 287, 35
Romanowsky, A. J., & Kochanek, C. S. 1998, ApJ, 493, 641
Romanowsky, A. J., & Kochanek, C. S. 1999, ApJ, 516, 18
Rybicki, G. B. 1978, in Structure and Dynamics of Elliptical Galaxies, ed. P. T. de Zeeuw (Dordrecht: Kluwer), 397
Schechter, P. L., Bailyn, C. D., Barr, R., et al. 1997, ApJ, 475, L85
Schwarzschild, M. 1979, ApJ, 232, 236
Sembach, K. R., & Tonry, J. L. 1996, AJ, 112, 797
Tonry, J. L. 1983, ApJ, 266, 58
Tonry, J. L. 1998, AJ, 115, 1