Next: Model validation Up: ShaneAO: Predicted performance limits Previous: Sky model
The telescope mirrors, AO and instrument optics are modeled as a series of gray bodies, each with emissivity
![]() , where
, where ![]() is the transmissivity/reflectivity of a surface. Transmission and reflection curves were either measured or supplied by manufacturers (such as ALPAO for the woofer). For surfaces without data, a flat curve was assumed across the wavelength band based on reasonable assumptions.
is the transmissivity/reflectivity of a surface. Transmission and reflection curves were either measured or supplied by manufacturers (such as ALPAO for the woofer). For surfaces without data, a flat curve was assumed across the wavelength band based on reasonable assumptions.
The effects of dust or degraded coatings, both a real problem at lower altitude sites like Lick Observatory, were modeled by modifying the emissivity or transmissivity of a surface as follows:
| (1) | |||
| (2) |
The telescope and AO system were set at a worst case ambient temperature of 18![]() C and the change in emissivity due to dust is applied to these surfaces. Instrument optics, filter wheels and the IR detector reside in a dewar cooled to -196
C and the change in emissivity due to dust is applied to these surfaces. Instrument optics, filter wheels and the IR detector reside in a dewar cooled to -196![]() C and are dust-free.
C and are dust-free.
The sky spectrum described above is propagated through each surface in the system. At any given surface, the upstream flux is reduced by the surface's reflectivity or transmissivity and the dust-modified emissivity of the surface is added. All pupil stops are assumed to behave perfectly for the ShaneAO system, so off-axis contributions to emissivity, from support structures for example, are ignored.
Hence, at each surface ![]() , the the flux in photons s
, the the flux in photons s![]() m
m![]() arcsec
arcsec![]() nm
nm![]() at a particular wavelength,
at a particular wavelength, ![]() , is given by:
, is given by:
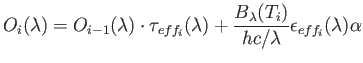 |
(3) |
where
![]() is Planck's blackbody function;
is Planck's blackbody function; ![]() ,
, ![]() and
and ![]() are the usual physical constants;
are the usual physical constants; ![]() is a unit conversion factor (it includes conversion from steradians to arcsec
is a unit conversion factor (it includes conversion from steradians to arcsec![]() among others). For a two-temperature system with
among others). For a two-temperature system with ![]() surfaces, the flux reaching the detector is given by:
surfaces, the flux reaching the detector is given by:
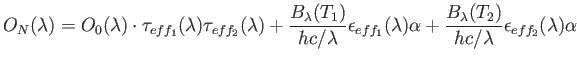 |
(4) |
where
![]() ,
,
![]() are the effective throughput and emissivity of the parts of the system at temperature
are the effective throughput and emissivity of the parts of the system at temperature ![]() (18
(18![]() C for the telescope and AO system, for this model).
C for the telescope and AO system, for this model).
At the detector, we assume diffraction limited imaging in each band and a flat-topped PSF scaled by the Strehl ratio. The collecting area of the telescope is that of the primary mirror with the area obscured by the secondary subtracted. Assuming the gain is set such that the ratio of incident photons to electrons in a well is 1:1, The noise due to the background is then the number of electrons in the Airy core generated by the sky and telescope emissivity in the time spanned by a Fowler-16 (IRCAL) or -32 (ShARCS) read.
Srikar Srinath 2013-10-09