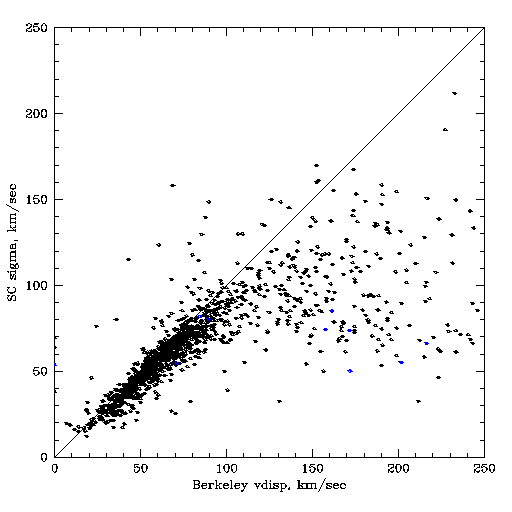
Dispersion from Gaussian fit vs dispersion from pipeline template fit
Ben Weiner 04/31/2003
This page compares emission-line velocity dispersions from DEEP2 first-season 1-d data, computed by two methods. The first is the dispersion produced by the Berkeley pipeline, through fitting of multiple broadened templates. The second is from automated fitting of Gaussians to individual emission lines, using a standalone program (referred to as "Santa Cruz" method strictly for convenience, not necessarily endorsed by others at UCSC).

Dispersion from Gaussian fit vs dispersion from pipeline template fit
1. Berkeley pipeline: A template Vdisp.fits in log wavelength is made by setting delta functions at the locations of emission lines and convolving with a gaussian of sigma_inst approx 28 km/s to approximate instrumental resolution. A series of broadened templates are generated by convolving Vdisp.fits with gaussians of sigma = 0,10,...,400 km/s. Relative line intensities are held fixed and the velocity offset is assumed zero. The spectrum is shifted to restframe log wavelength and each template is fit to it, producing the run of chi-squared with sigma. A spline fit is used to find the minimum in chi-sq, and the error comes from a delta-chisq=1 criterion (I think).
This is from the procedures spec1d/pro/vdispfit.pro and findchi2min.pro. Corrections are welcome. This procedure uses the optimally-extracted spectrum.
2. "Santa Cruz" Gaussian fits: The program finds the expected locations of each of a short list of features and fits a Gaussian to each line. The fit to each line is independent. For the [O II] 3727 doublet, a double gaussian is fit and the line ratio is free to vary. The parameters for each line are continuum, intensity, velocity offset from nominal redshift, and dispersion. (Dispersions less than the instrumental are allowed, but rarely found in 4 sigma or greater detections.) The fit is a standard non-linear least squares routine, mrqmin from Numerical Recipes, and produces error estimates. For each object, if it had multiple lines I used the highest intensity line to get the dispersion. Only 4 sigma detections are used. The instrumental resolution assumed is sigma_inst = 0.63 A. (obtained by looking at SKYSIGMA from Berkeley pipeline v1_1 on a few masks). This used the boxcar-extracted spectrum.
The plots below compare dispersions for a sample of galaxies with both dispersion estimates. The "Santa Cruz" dispersion comes from gaussian fits for objects in fields 2 and 3, v1_0 reductions, with 4 sigma detections. This list was matched to Berkeley dispersions from the file zcat.v1_0.fits. There were 1553 objects in the SC list, 1473 matches, 1265 had good Berkeley dispersions; the others presumably do not reach a minimum in chi-squared(sigma). Because the SC list is a subset, I did not count how many objects had a good Berkeley measure and a bad SC measure, but that is equally important.
1. There are a number of objects for which the Berkeley dispersion is much higher than the SC dispersion. This is worst for high-dispersion objects and seems to affect nearly all objects with Berkeley disp above 100 km/sec.
2. There appears to be an offset in the sense that Berkeley disp is a little higher than SC. Could this be related to optimal versus boxcar extractions, or to splining the chi-squared(sigma) ?
3. There is a systematic difference trend with z. Perhaps related to optimal versus boxcar if relative weighting, window sizes and z are related? If so that is potentially a big issue. (There is the old airtovac wavelength issue, since these are v1_0 reductions, but it's hard to see how that could produce such a big difference.)
4. There appears to be a weak systematic difference with observed wavelength, in the expected direction. But they don't agree at 6750 A, due to the systematic offset.
5. Apart from the issues above the distribution of (Berkdisp - SCdisp) is basically consistent with the error estimates (plot not shown).
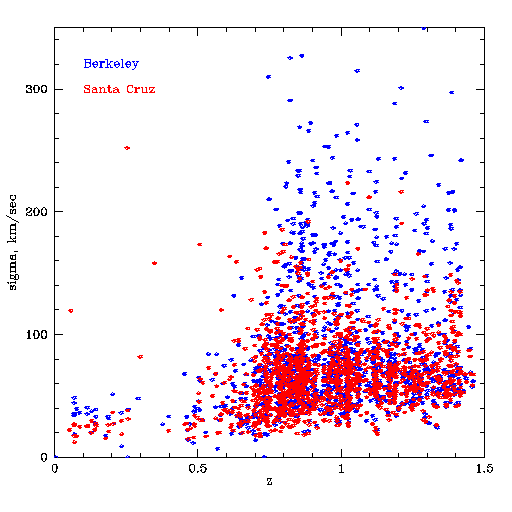
Dispersion vs redshift

Dispersion vs dispersion: high dispersion problem
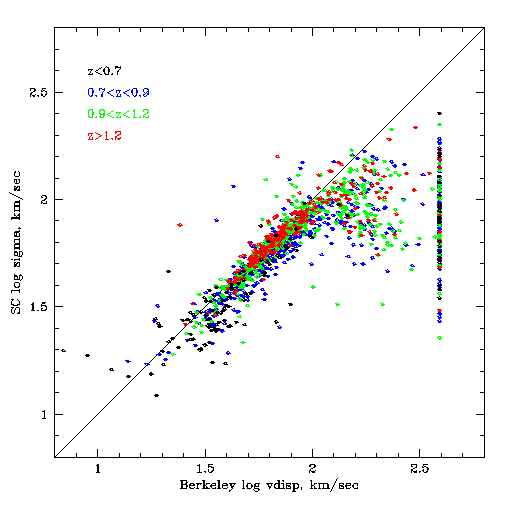
log dispersion vs log dispersion, colored by z range
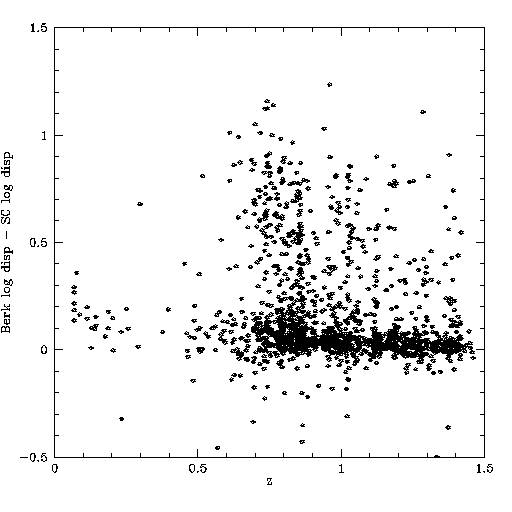
Difference in log dispersion, as function of z; trend with z
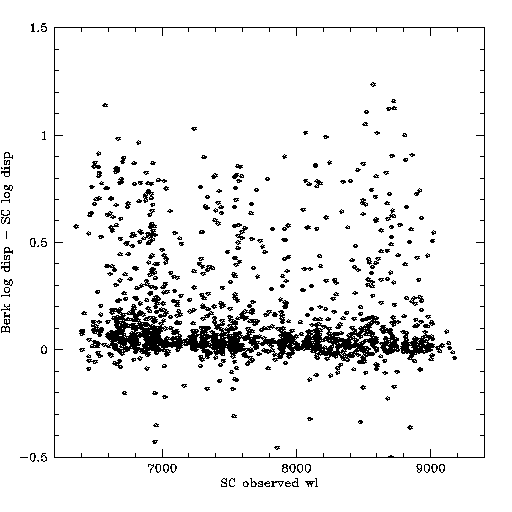
Difference in log dispersion, as function of observed wavelength; weak trend
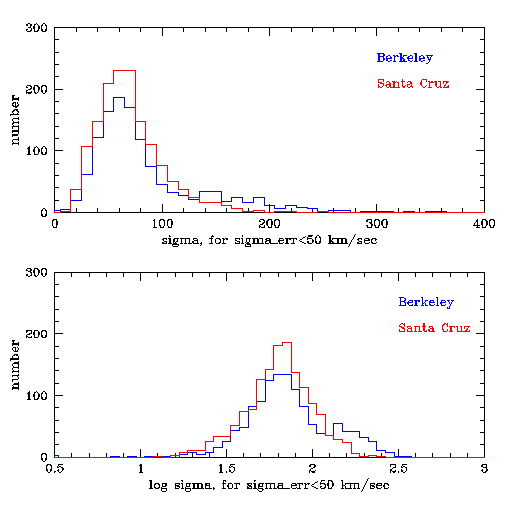
Histograms of dispersion
mask.object z Bdisp err SCdisp err SC_line_used 2200.22016331 0.846 123.6 10.3 72.6 4.3 3728 2200.22031491 0.981 152.3 5.8 108.1 5.8 3728 2200.22031547 0.870 152.6 8.0 88.5 4.3 3728 2243.22060813 0.625 131.5 0.7 94.8 1.9 5007 2258.22025284 1.041 215 28.3 58.3 6.1 3728 low S/N 2280.22024423 0.827 183.3 15.3 94.6 9.7 3728 2280.22031928 1.057 152.3 5.5 169.8 5.8 3728 SC fit bad due to fitting a broad singlet to [O II], non gaussian lineshape 3202.32022827 0.743 130.3 2.4 80.4 2.8 5007
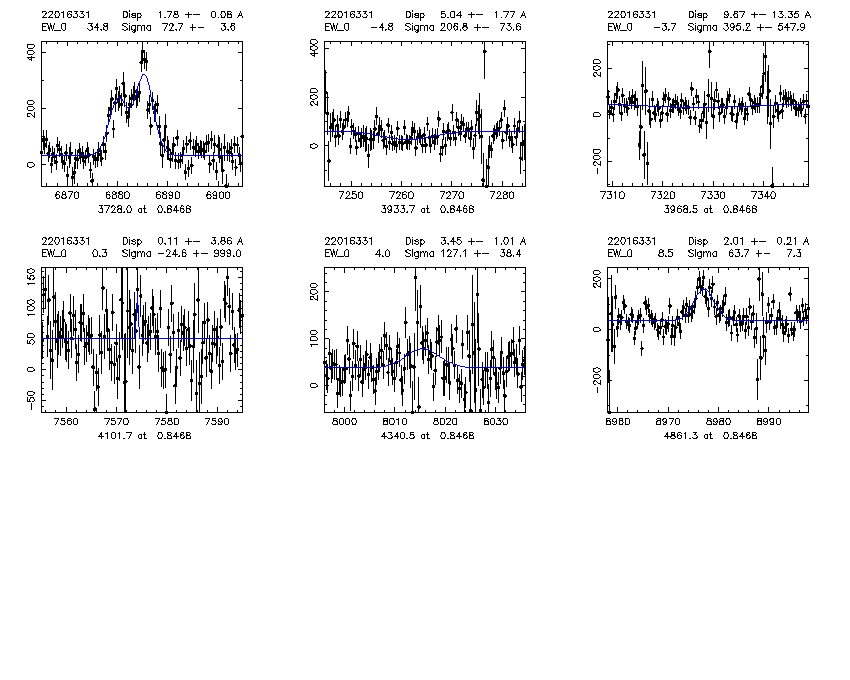 2200.22016331
2200.22016331
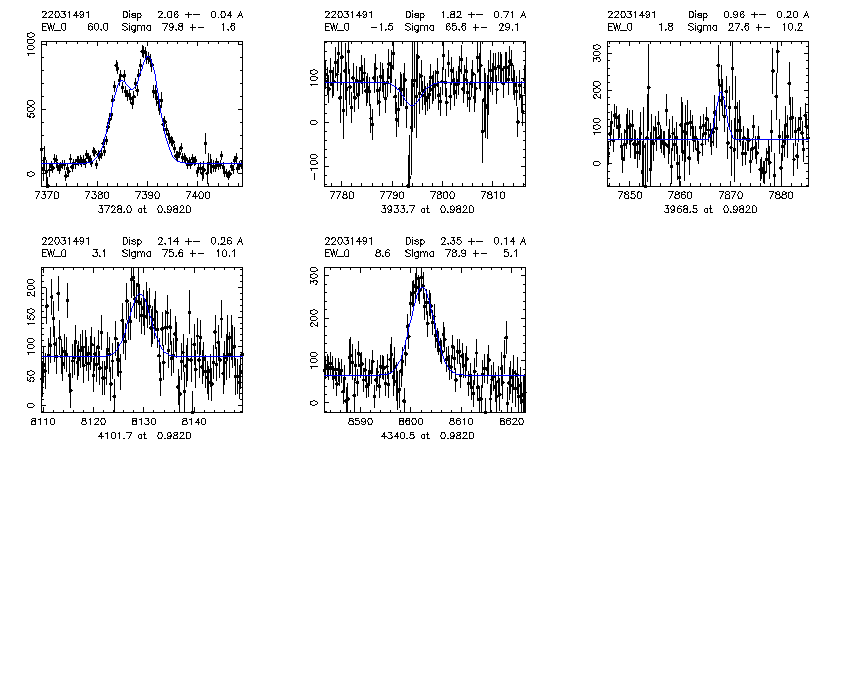 2200.22031491
2200.22031491
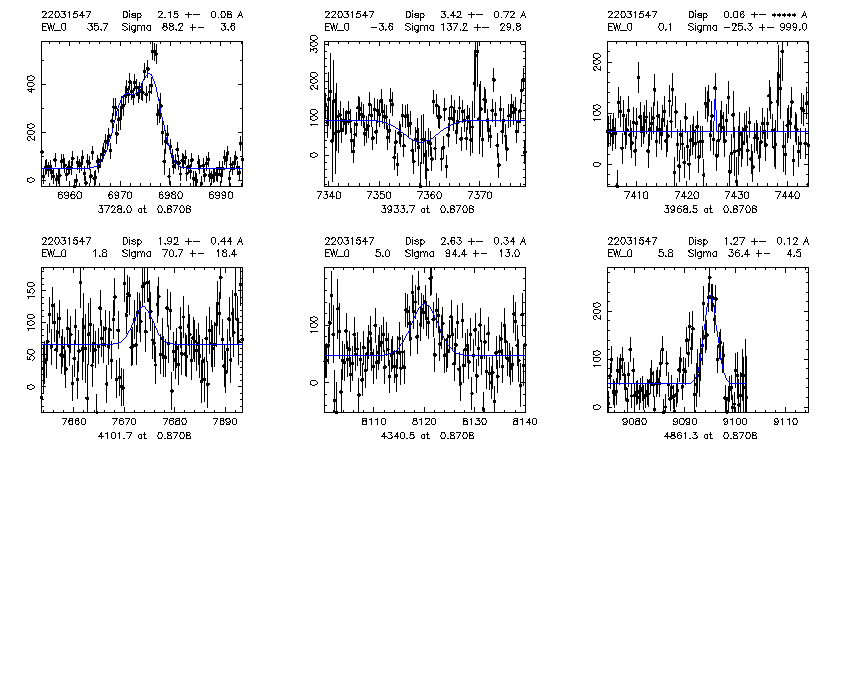 2200.22031547
2200.22031547
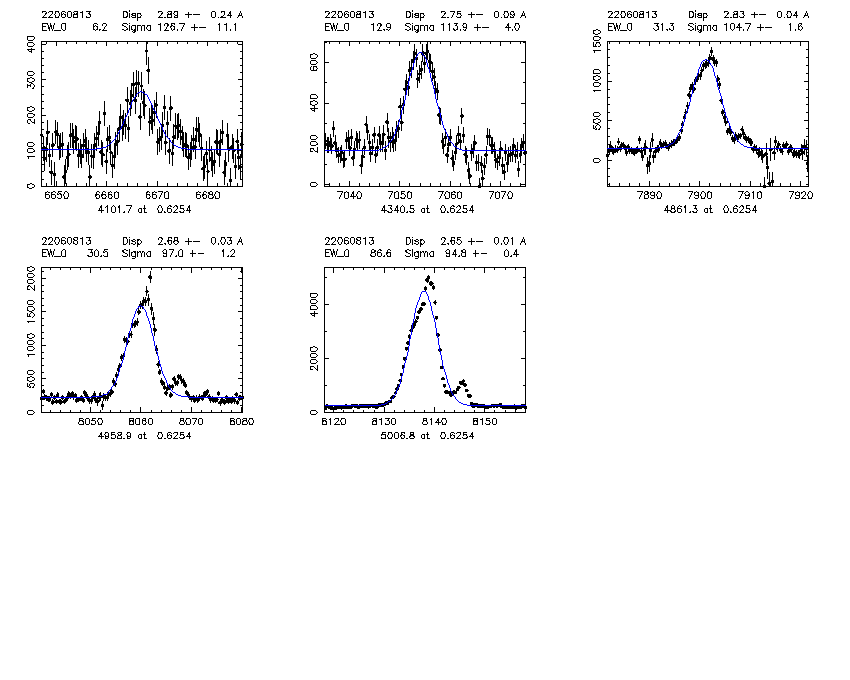 2243.22060813
2243.22060813
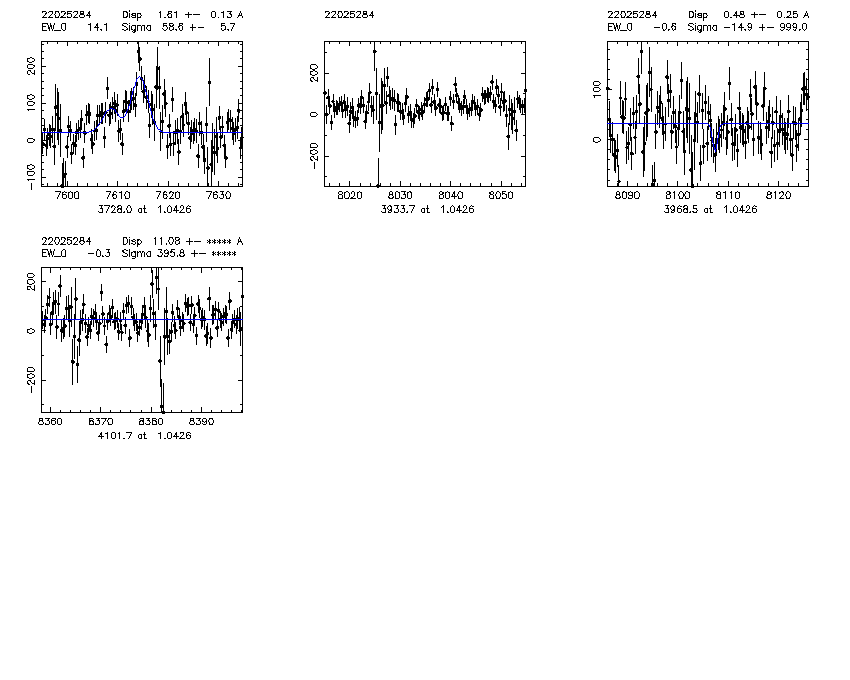 2258.22025284
2258.22025284
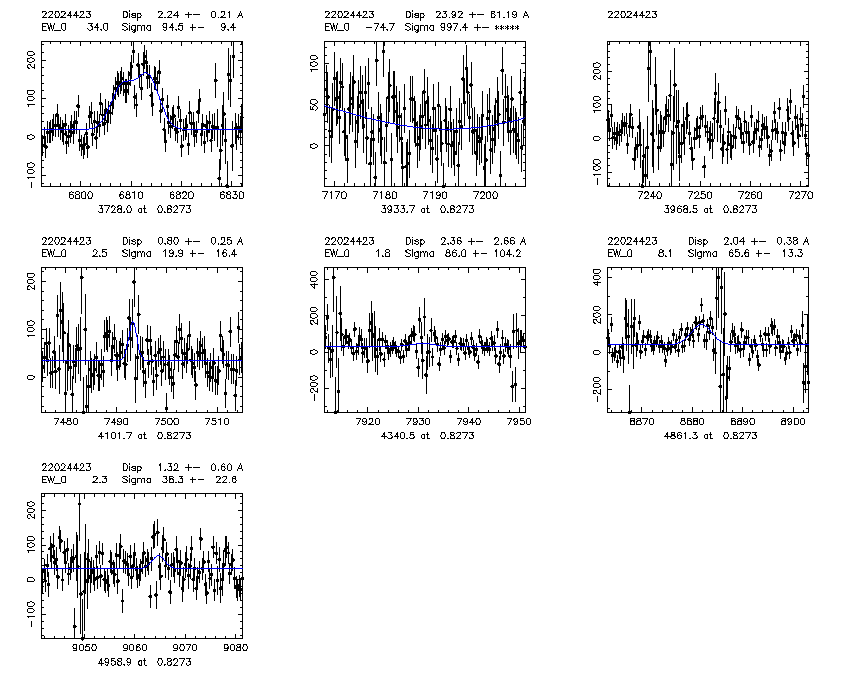 2280.22024423
2280.22024423
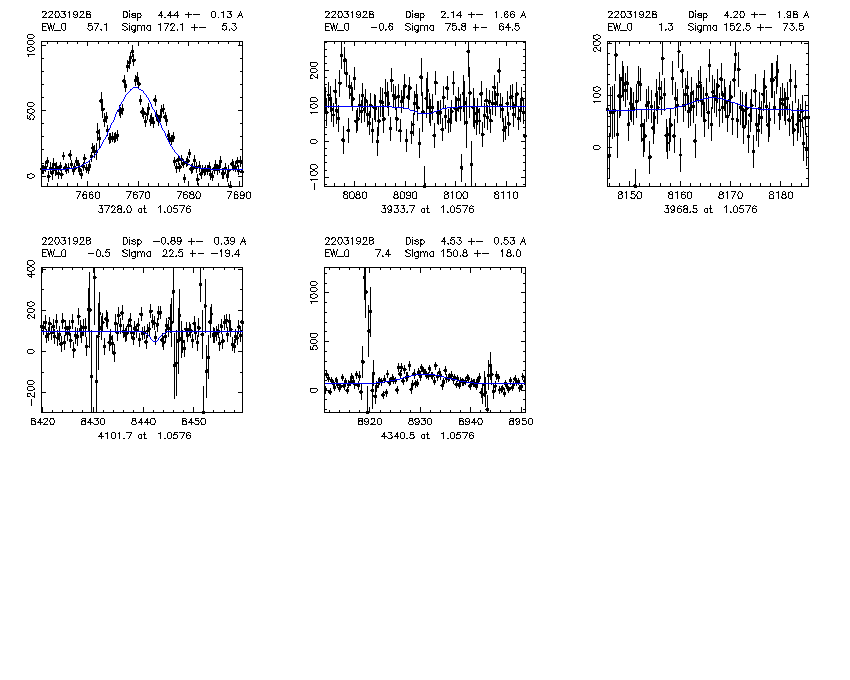 2280.22031928 - bad fit, non Gaussian lineshape, more like the sum of two offset doublets
2280.22031928 - bad fit, non Gaussian lineshape, more like the sum of two offset doublets
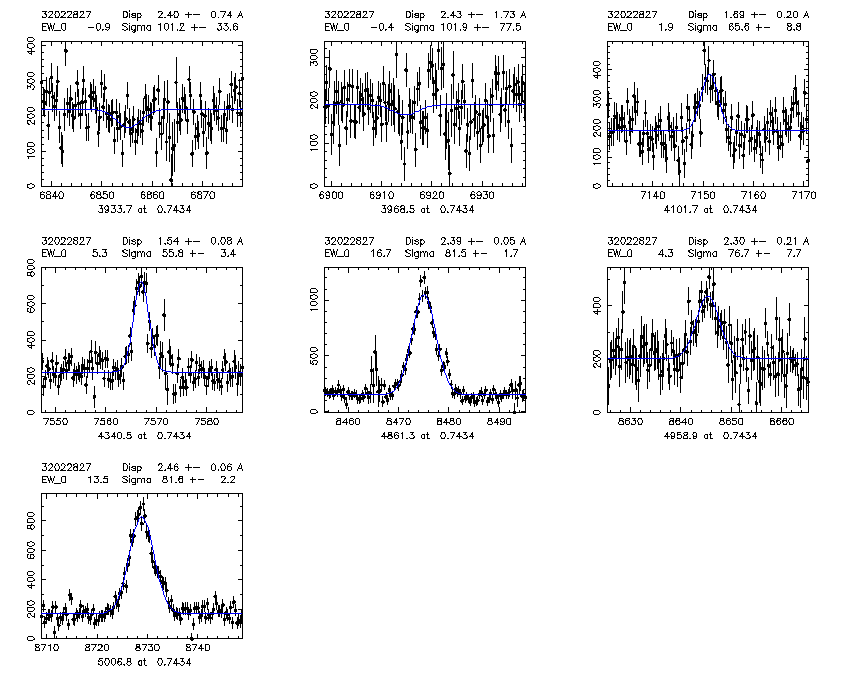 3202.32022827
3202.32022827
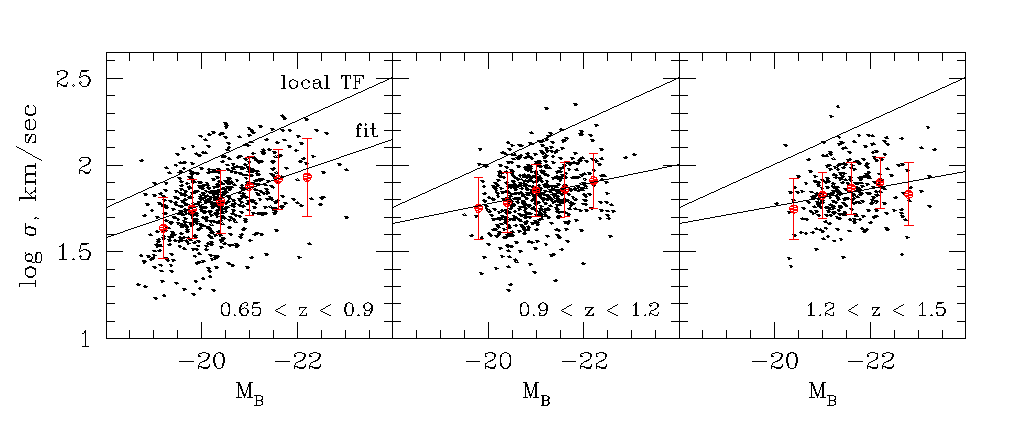
DEEP 2 linewidth-magnitude relation