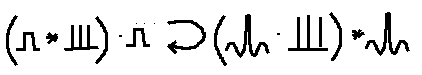
The above is a picture of the Fourier optics of a diffraction grating. The first symbol is the boxcar function. The next one is the comb function, which is an infinite set of delta functions. The star is the convolution operator. The result of the convolution is that the object in parens is an infinite row of boxcar functions, the slits in the grating. These are then multiplied by another boxcar function to make the grating of finite length.

The curly arrow is my symbol for Fourier transform. In optics one needs to do repeated transforms, so one cannot use the usual capitalization convention for transforms.

In the transform domain this goes to another comb function. Each of these deltas is what you call an "order" in the diffraction pattern. The orders are multiplied by the transform of the boxcar, sin(x)/x. This is called the visibility function. Then the orders are convolved by the transform of the boxcar which gave the finite size to the grating, to spread the spots out.

The transform domain picture is what you see when you let the light propagate a large distance (out of the fresnel domain), or look at it in a telescope ("from infinity").

Thanks to Bruce Robbins. When I had drawn the above "equation" on the board he cried out, "Stop. Stop. Wait just a minute. I didn't sign on for a class in egyptology. Look at what you just wrote."
Check out:

1. Bracewell, Ronald Newbold, 1921-

The Fourier transform and its applications / Ronald N. Bracewell. 2nd ed., rev. New York : McGraw-Hill, c1986.

UCSC Science QA403.5 .B7 1986