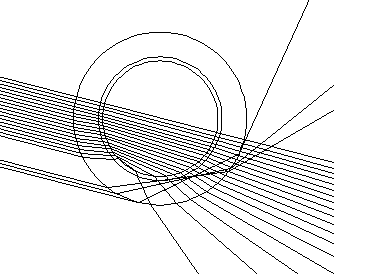
To explain this you need to use the spherical version of Snell's Law.

Ray trace of the situation.

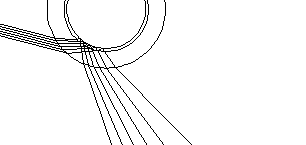The rays which form the shiny image of the envelope. These were left out of the drawing above.

The circular version of Snell's law states that along a ray

n r sin \theta

is constant. The term

r sin \theta

is the impact parameter. The first ray to penetrate the glass envelope and let you see the frosting is back in a region of index 1.0, and so has the same apparent size as the true size of the region. The ray which just misses the envelope completely has nearly the same impact parameter (modulo the thickness of the glass envelope) but since the ray is in water, the conserved quantity is larger by a factor of the index of refraction of water. In air, then, the envelope, which appears to be between these two rays, has a size (n-1) r.

Mark Nockleby showed me a lightbulb for which this does not work. How can that be?

See also,

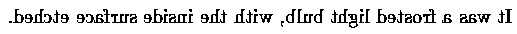
The Not-So-Short Beer

William Burke

American Journal of Physics, 48, 783 (1980).

Thanks to Mike Edwards for showing me how to make transparent gif's.