Multidimensional Modeling of Type I X-ray Bursts. I. Two-Dimensional Convection Prior to the Outburst of a Pure He Accretor

Malone, C. M., Nonaka, A. J., Almgren, A. S., Bell, J. B., & Zingale, M., (2010) submitted to ApJ

We present multidimensional simulations of the early convective phase preceding ignition in a Type I X-ray burst using the low Mach number hydrodynamics code, MAESTRO. A low Mach number approach is necessary in order to perform long-time integration required to study such phenomena. Using MAESTRO, we are able to capture the expansion of the atmosphere due to large-scale heating while capturing local compressibility effects such as those due to reactions and thermal diffusion. We also discuss the preparation of one-dimensional initial models and the subsequent mapping into our multidimensional framework. In our multidimensional simulations, we find that the resolution necessary to properly resolve the burning layer is an order of magnitude greater than that used in earlier studies. We characterize the convective patterns that form and discuss their resulting influence on the state of the convective region, which is important in modeling the outburst itself.

Simulation Details

Type I X-ray bursts (XRBs) are a result of thermonuclear burning in the accreted atmosphere of a neutron star in a mass-transferring low mass x-ray binary system. The thermonuclear burning begins at the base of the accreted layer where the temperature and density are highest in the fuel. This burning drives very subsonic convection throughout the overlying material. Eventually, the nuclear burning becomes so violent that convection can no longer efficiently transport the energy away from the burning layer, and a burning front is born, which will propagate around the surface of the star. At the ignition densities inferred from most burst sources, the burning front will propagate as a subsonic front, i.e., a deflagration.

Low Mach number flows are notoriously expensive to simulate with traditional fully compressible hydrodynamics algorithms, such as FLASH, because of the propagation of unimportant accoustic waves that limit the timestep size for numerical stability reasons. There exist methods called low Mach number approximation methods, which filter accoustic waves from the system and allow for an increase in timestep size (e.g., by a factor of 1/M where M is the Mach number) thus making long term evolution feasible. A common example of a low Mach number approximation is that of an incompressible fluid; this approximation, however, does not allow for important compressible effects such as expansion of a fluid element as it rises in a stratified background. We make use of a low Mach number approximation code, MAESTRO, whose algorithm allows for important compressibility effects such as those due to reactions, thermal diffusion and compositional changes. This code was specifically written for simulating low Mach number astrophysical fluid flows in either 2- or 3-d atmospheres or full stars. Our method differs from that of Lin et al. in that MAESTRO is 2nd order accurate in both space and time and allows for modeling of low density regions (i.e., the surface) by adapting a sponging technique from the atmospheric modeling community which dampens spurious velocity generation in these regions. Furthermore, MAESTRO includes a time dependent hydrostatic background state with allows us to capture the expansion due to heating — this will be critical to understanding so-called photospheric radius expansion (PRE) bursts in future studies.

To construct an initial one-dimeionsal model we construct a pure Helium-4 atmosphere in hydrostatic and thermal equilibria on the surface of a pure nickel-56 neutron star much in the spirit of Cumming and Bildsten (2000). We check for the thermal instability criterion

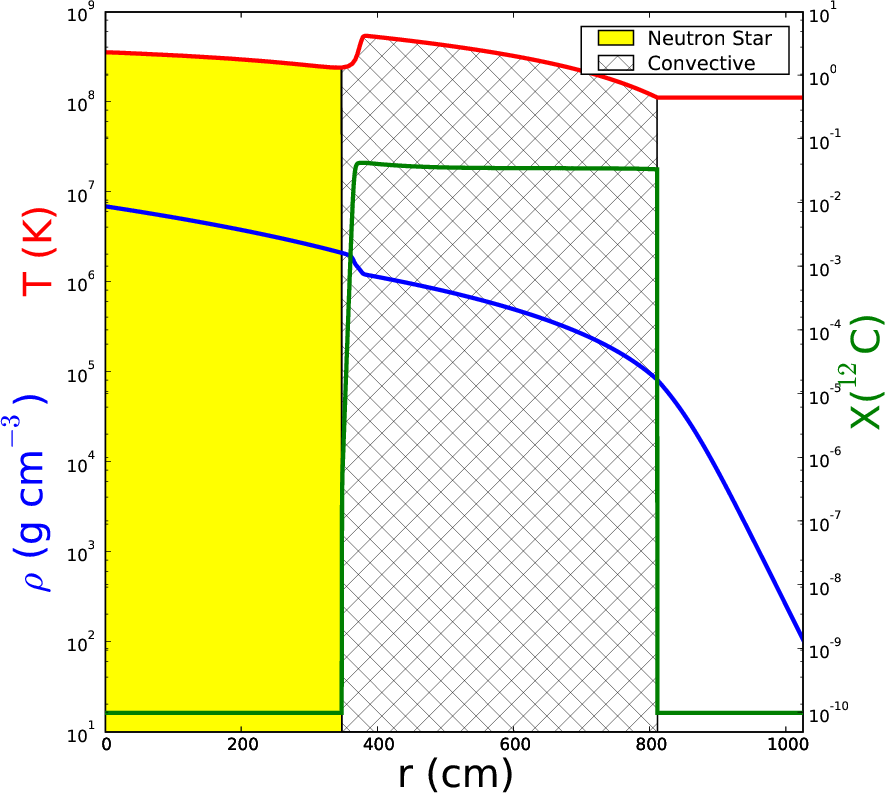
essentially where the energy generation rate is more temperature sensitive than the local cooling rate, which is approximated by the rate at which conduction and radiation can transport the heat. In multiple dimensions, another way the fluid can cool is via convection which would alter the local cooling rate and may make the system no longer thermall unstable. To approximate the local cooling due to convection, we asked Stan Woosley to map our model into his one-dimensional stellar evolution code, Kepler, and let the system evolve using a mixing-length-theory prescription for the convection. Stan kindly evolved our model and allowed the 3-α burning to heat the base of the accreted layer and produce a well mixed Carbon-12 region. Figure 1 shows the result of this evolution.

Results

When we mapped the model in Figure 1 in multiple dimensions, we found that the resolution required to properly resolve the thin burning layer was on the order of 0.5 cm zone^-1—this is an order of magnitude greater than what what was used in the Lin et al. studies. It is important to note that our initial models are different from those of Lin et al. In particular, their models only considered two species—the accreted layer was pure Helium and the underlying neutron star was composed entirely of Carbon. This caused their models to have a smaller jump in mean molecular weight across the neutron star/accreted layer boundary compared to our models. Furthermore, the initial conditions for their multidimensional studies were from the results of a one-dimensional diffusional-thermal code that evolved the system through several bursts. These differences from our method of initial model generation give the Lin et al. models an extended (~ 100 cm) thermal peak compared to our narrow (~10 cm) peak. Here we are defining the width of the peak to be the distance between points which are 90% of the maximum value of temperature—this is a good measure because the 3-α reaction rate is extremely temperature sensitive in this burning region (something like T⁴⁰).

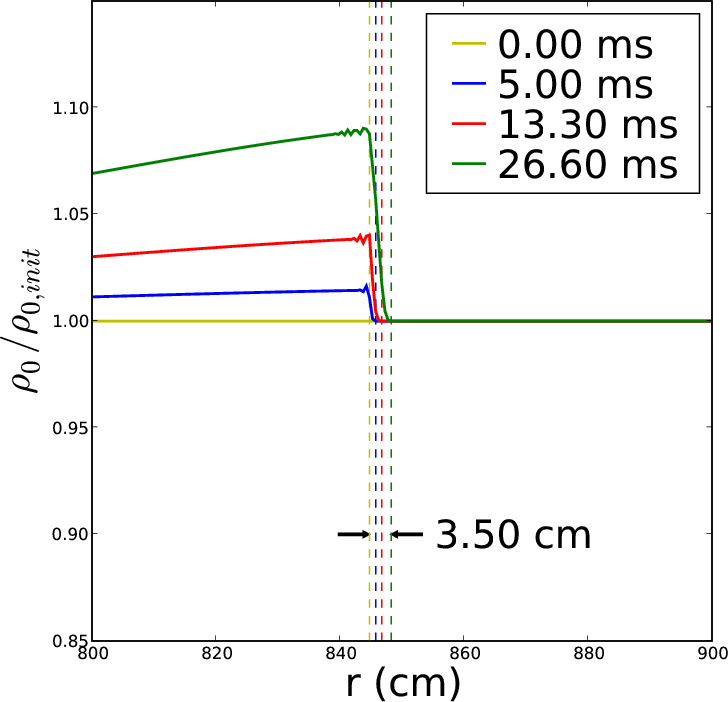
By including a time dependent hydrostatic background state we can capture the expansion of the atmosphere due to heating. Figure 2 shows that in our simulations, the background expanded by ~3.5 cm in about 30 ms of evolution. In this plot, ρ₀(r,t) is the background density at time t and ρ_0,init is the density at t=0. Although this seems small at these early times, the rate of expansion increases as the burning progresses. If we could evolve the system until the actual non-linear burning regime, we would be able to simulate a PRE burst and discuss the extent and location of the photosphere—this is critical to using such bursts to determine the mass and radius of the neutron star (see for example, Steiner et al.).

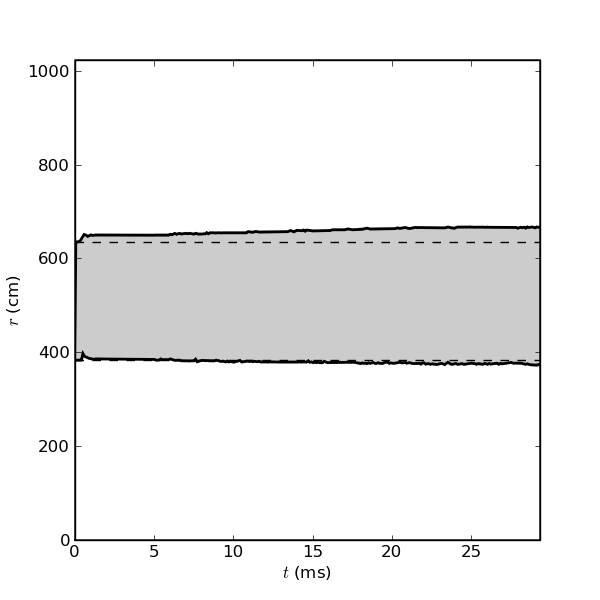
The convective dynamics that form are complex and turbulent. The gif at the top of this page shows the initial adjustment of the Carbon-12 mass fraction in the convective zone. We start the simulation with no multidimensional velocity information from the Kepler simulation—the convective zone needs to adjust from its 1-d configuration into a configuration which is convectively unstable in 2-d. At later times like those shown in Figure 3, the convective region becomes well defined. Figure 4 shows the evolution of the convective goundary as a function of time. For the 30 ms duration of this simulation, the upper convective boundary expands outward by 32.5cm while the lower boundary moves inward by 9.5 cm.

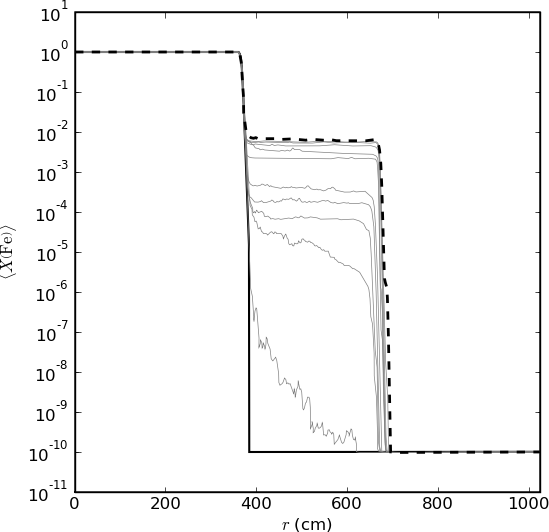
In 2-d the turbulence is such that small vortices tend to clump together and merge forming a single dominant vortex. This effect can noted in Figure 3 by the fact that many of the Carbon-12 over-densities disappear leaving only a few well formed cirulation patterns. Figure 5 shows a single timeslice of the gif in Figure 3 but also includes velocity vectors. As the smaller vortices merge, they form the larger vortices that dominate the flow. When the have grown large enough, the vortices begin interacting with the lower convective boundary at the atmosphere/neturon star interface and shearing occurs. This churns up the underlying Iron-56 material into the convective region and slightly alters its conductivity. Figure 6 shows the evolution of the Iron-56 distribution as a function of time going from the initial configuration (solid) through to the end of the simulation (dashed).

Future Work

The next logical step would be to perform these simulations in 3-dimensions and compare the turbulent convection seen there to our results in this paper; we are currently investigating this. Also, we are getting ready to run some mixed Hydrogen/Helium burst models to see how things differ; ideally, the resolution requirements for the mixed bursts will be relaxed because of the less temperature sensitive reaction rates involved. Additionally, there are several methods in the literature for calculating the conductivities used at the high temperatures and densities found in the XRB problem and unfortunately they disagree by, in some cases, an order of magnitude. It would be nice to study how these differences could affect the soltion of the convective dynamics and to further catalog the various conductivity routines in a publicly available fashion.

Acknowledgements

We thank Frank Timmes for making his conductivity and equation of state routines publicly available and Ed Brown for useful discussions regarding the possibility of relaxed resolution requirements for H burning. We also thank Andrew Cumming for providing the initial semi-analytic models and Stan Woosley for using the Kepler code to augment these models. The work at Stony Brook was supported by a DOE/Office of Nuclear Physics Outstanding Junior Investigator award, grant No. DE-FG02-06ER41448, to Stony Brook. The work at LBNL. was supported by the SciDAC Program of the DOE Office of Mathematics, Information, and Computational Sciences under the U.S. Department of Energy under contract No. DE-AC02-05CH11231. This research utilized resources at the New York Center for Computational Sciences at Stony Brook University/Brookhaven National Laboratory, which is supported by the U.S. Department of Energy under Contract No. DE-AC02-98CH10886 and by the State of New York. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231.

Plot of the Carbon-12 mass fraction in the convective region for t < 1.3 ms.

Figure 1: Initial 1-d model. The well mixed Carbon-12 region shows the extent of the convective zone determined from the mixing-length-theory prescription used in the Kepler code.

Figure 2: Close up of the background density near the surface of the star. By utilizing a time dependent background state, we are able to capture the small (3.5 cm) expansion of the atmosphere due to heating from nuclear reactions below.

Figure 3: Same as gif at the top of the page but at later times, 5 ms ≤ t ≤ 25 ms, while the convective zone becomes more established.

Figure 4: Extent of the convective zone. The horizontal lines indicate the initial extent. As the system evolves, the convective zone expands in both directions, but the upper boundary expands upward more than 3 times as fast as the lower boundary does downward.

Figure 5: Timeslice at t=23 ms of the gif in Figure 3 showing velocity vectors. Clearly there is one dominant vortex with a few smaller vortices. As the vortices grown and are advected around the fluid, they begin to interact with the lower convective boundary and shearing occurs.

Figure 6: Iron-56 mass fraction as the system evolves from the initial distribution (solid line) to the end of the simulation (dashed line). As the vortices interact with the lower boundary, Iron-56 is churned up into the convective region.