Ph 258, Ay 258: Class Webpage

Applied Differential Geometry

Go to Bill Burke's home page.

Contents

Class Information

Astronomy/Physics 258 Working Class Schedule and Index to Related Material

Rescheduling the rest of the quarter in light of the reality that we are not going to get textbooks. Thus I plan to switch over to following the preliminary edition of Div Grad Curl Are Dead. Numbers in square brackets refer to sections in DGCAD. Old schedule.

Mathematica Calculator for Differential Forms

Here is a simple calculator written in mathematica for manipulating differential forms expressions. The mathematica rules. and PostScript User's Manual.

References.

Here are books that I mention in class.

Evaluation

Your class evaluation will depend on nearly weekly problem sets.

Writing mathematics as a text stream

Here are some remarks on writing mathematics over email or in HTML.

Suggestions for mathematica users.

Mathematica solution.

  • (30) For the above dispersion relation, invent and solve several routine exercises, in the 10-15 range.

    Problem Set 2

    1. (15) Draw a picture of the tensor

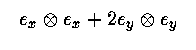
      (Hint: you might want to first work the case of a similar tensor defined using basis covectors rather than basis vectors.)

    2. Describe the metric represented by the tensor

      du dv + dv du.

      Solution to the above two problems.

    3. (14) What angle does an observer moving in the x + y + z direction with speed v see between two light rays coming from the x and the y directions?

    4. (Optional, open ended) Fed up with it all, you decide to flee the galaxy. You depart perpendicular to the plane of the galaxy at one g acceleration. Describe the changing appearance of the galaxy for the rest of your lifetime. (Stolen from Hoyle and Hoyle, Into Deepest Space).

    Problem Set 3

    1. (25) Find coordinate charts for all of the manifold M whose points are pairs: points in 3-space and planes passing through that point.

    2. (30) Describe the map from S^2 to M, the surface of the sphere to the space above, which assigns to each point on the sphere the pair: that point in 3-space corresponding to the sphere of unit radius, and the plane tangent to the sphere at that point. Describe the map both using homogeneous coordinates wherever possible, and also using charts for both spaces.

    Solutions.

    Problem Set 4

    1. (18) In the discussion to come (pg 132) on parking a car we will need to work out the following commutators (t for theta, p for phi). Starting with a vector field
      STEER = d/dp
      and a vector field
      DRIVE = cos t d/dx + sin t d/dy + tan p d/dt
      in a four dimensional configuration space (x,y,t,p), work out their commutator, and then the commutators with that, until the process closes. Do you end up with enough vectors to span all possible directions?

      Solution.

    2. (18) A map from R^3 to the future timelike unit hyperboloid in spacetime:
      t^2 - x^2 - y^2 - z^2 = 1
      is given by, using polar coordinates in R^3:
      (r,th,p) \mapsto
      t = cosh r
      z = sinh r cos th
      x = sinh r sin th cos p
      y = sinh r sin th sin p
      Pullback the metric of spacetime, to find a metric tensor on R^3.

    Problem Set 5

    Solutions.
    1. For the 3-manifold discussed last week, the future timelike hyperboloid in spacetime, call it H:
      (i) show that the transformations:
      R = x d/dy - y d/dx
      X = x d/dt + t d/dx
      Y = y d/dt + t d/dy
      are all symmetries of 4-D spacetime;

      (ii) show that at every point of H the above vectors lie in the hypersurface, which means that the vectors can be "pulled back" to H;

      (iii) show that the above vector fields are symmetries of H.

    2. Consider a double pendulum, both rods of length L, both bobs of mass M. Suppose each rod is free to rotate in a full circle.
      (i) what manifold describes the configurations ?

      (ii) use coordinates (u,v), where u is the angle of the top rod from the vertical, and v is the angle of the second rod from the vertical. What ranges are appropriate for u and v?

      (iii) Suppose gravity acts. What is the potential energy function? Sketch the force 1-form at a few points.

      (iv) Suppose a force acts horizontally on the top bob. What is the potential energy function?

      (v) Suppose a force acts horizontally on the bottom bob. What is the force 1-form? Figure it out from the principle of virtual work, and explain this in our language.

      (vi) Find equilibria for the above two cases.

      (v) (Optional) Show that the above two cases are consistent with the reciprocity theorem.

    Problem Set 6

    1. Translate the Lorentz force law: F = q(E + v x B) into differential forms. F and E will be 1-forms, q just a number.
    2. Describe traffic flow in (x,y,t) spacetime. Use a twisted 2-form. What 2-form corresponds to traffic moving with the x component of velocity u, and y component v, and
      (i) spatial density \rho
      (ii) flux across the x=constant planes of k.
      Set up a "right-hand-rule" and show how one can use an untwisted 2-form can be used in the above situation.

    Problem Set 7

    1. For the square-in-square capacitance example (DGCAD pg 33.3), what can you learn from a trial function which distributes charge uniformly on the outer surface, and has flux tubes which are radial?