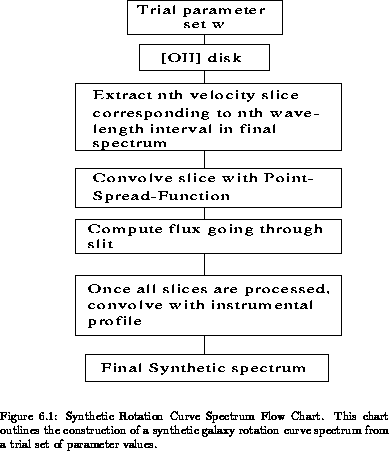
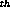 pixel along the dispersion axis is bounded by two wavelengths,
pixel along the dispersion axis is bounded by two wavelengths, 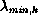 and
and 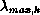 , corresponding to two velocities, V
, corresponding to two velocities, V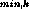 and V
and V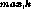 . This velocity window was used to build a narrow-band image of the simulated disks from [OII] fluxes at locations with projected velocities between V
. This velocity window was used to build a narrow-band image of the simulated disks from [OII] fluxes at locations with projected velocities between V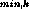 and V
and V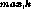 .
.